RootMe - RSA Factorisation
Task Overview
The validation password was encrypted using this public key (pubkey.pem).
Ciphertext :
e8oQDihsmkvjT3sZe+EE8lwNvBEsFegYF6+OOFOiR6gMtMZxxba/bIgLUD8pV3yEf0gOOfHuB5bC3vQmo7bE4PcIKfpFGZBA
RSA Overview
RSA algorithm allows to:
- generate two related with each other keys: public key and private key.
- use that two keys during information exchange
Public key is used to encrypt message, private key is used to decrypt message.
Key generation
- Generate in secure way two big prime integers.
- Calculate n = p*q
- Calculate Euler’s totient for n
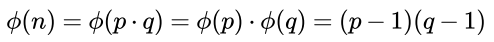
- Choose
ewhich meets requirements:1 < e < Euler's TotientANDGCD(e,Euler's Totient) = 1.eis public key exponent. - Choose
dsuch that:d*e=1 mod Euler's Totient.dis private key exponent.
Finally, we got:
- public key components
(e,n) - private key components
(d,n)
Encryption
As mentioned above, encryption is done with public key (e,n). To encrypt plain text T and receive ciphertext C we need to perform below operation:
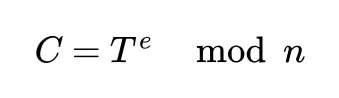
Decryption
Decrypting is performed with private key (d,n), to decrypt ciphertext C and receive plain text T we need to perfrom below operation:
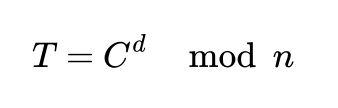
Theoretical solution
So, now we know how RSA cryptosystem works. We want to decrypt ciphertext C, to do that we need:
- Plain text
T n- result of multiplaction of two big integerspandqd- private exponent
Author of that task gave us public key (so we have n and e) and plain text (T). The last thing we need is d number, which is component of private key. However we don’t now that value, but we know that d is calculated according to formula: d*e=1 mod Euler's Totient. Unfortunately, we come up with next problem Euler’s Totient value is unknown. But again, we can calculate it with formula mentioned here. However this is not easy, because we need to know exact values of p and q which are factors o n value. We can try to factorise n value with algorithms such as:
- Rho-Pollard factorisation
- Feramt factorisation
- Shamir factorisation, etc.
In our case, this number is kinda big, so we will use factordb.com to get values of p and q.
Enough of theory, let’s go!
Practictal solution
Getting p and q
First of all, we need to get (e,n) values, we can do that with openssl tool.
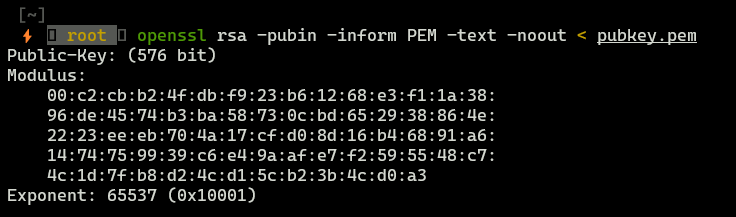
So e=65537 and n=C2CBB24FDBF923B61268E3F11A3896DE4574B3BA58730CBD652938864E2223EEEB704A17CFD08D16B46891A61474759939C6E49AAFE7F2595548C74C1D7FB8D24CD15CB23B4CD0A3 (in hex, decimal value was too big to paste it here). Let’s factorise n.

p=398075086424064937397125500550386491199064362342526708406385189575946388957261768583317q=472772146107435302536223071973048224632914695302097116459852171130520711256363590397527
Building private key
We can write simple python script to determine private key.
from Crypto.PublicKey import RSA
from Crypto.Util.number import inverse
def write_file(file_name, content):
with open(file_name, "wb") as file:
temp = file.write(content)
def calculate_d(e,p,q):
eulers_totient = (p-1)(q-1)
d = inverse(e, eulers_totient)
return d
def buid_priv_key(n,e,d,p,q):
key = RSA.construct((n, e, d, p, q))
write_file("private.pem",key.export_key()) # writing key to file
if __name__ == '__main__':
e = 65537
n = 0xC2CBB24FDBF923B61268E3F11A3896DE4574B3BA58730CBD652938864E2223EEEB704A17CFD08D16B46891A61474759939C6E49AAFE7F2595548C74C1D7FB8D24CD15CB23B4CD0A3
p = 398075086424064937397125500550386491199064362342526708406385189575946388957261768583317
q = 472772146107435302536223071973048224632914695302097116459852171130520711256363590397527
# calculating private component
d = calculate_d(e,p,q)
buid_priv_key(n,e,d,p,q)
Getting decrypted message
I used https://8gwifi.org/rsafunctions.jsp to decrypt ciphertext.
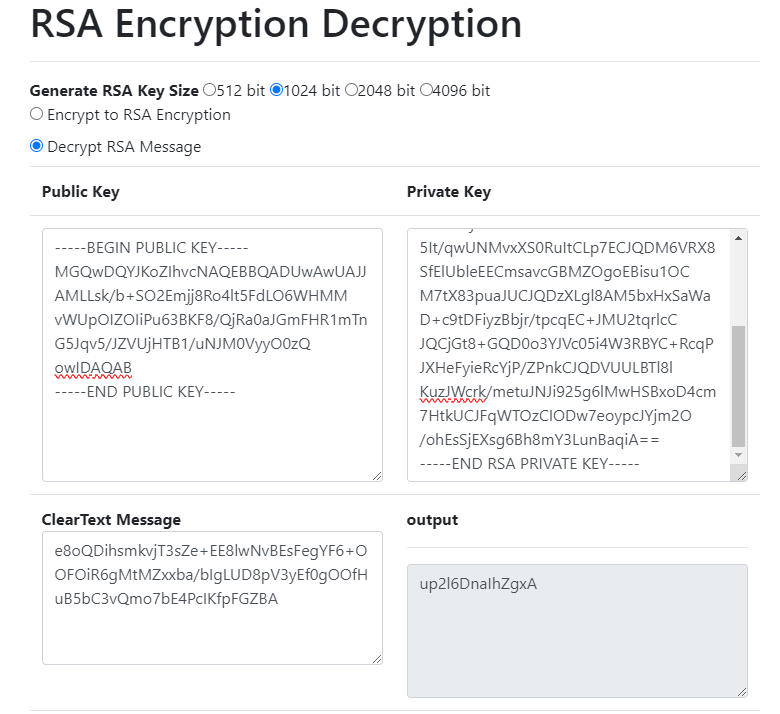
And finally we got our flag!