picoCTF 2021- Mind your Ps and Qs

If you read writeup to ‘RootMe - RSA Factorisation’, you can skip below section :).

RSA Overview

RSA algorithm allows to:

• generate two related with each other keys: public key and private key.
• use that two keys during information exchange

Public key is used to encrypt message, private key is used to decrypt message.

Key generation

1. Generate in secure way two big prime integers.
2. Calculate n = p*q
3. Calculate Euler’s totient for n

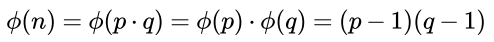
1. Choose e which meets requirements: 1 < e < Euler's Totient AND GCD(e,Euler's Totient) = 1. e is public key exponent.
2. Choose d such that: d*e=1 mod Euler's Totient. d is private key exponent.

Finally, we got:

• public key components (e,n)
• private key components (d,n)

Encryption

As mentioned above, encryption is done with public key (e,n). To encrypt plain text T and receive ciphertext C we need to perform below operation:

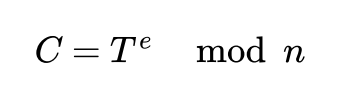
Decryption

Decrypting is performed with private key (d,n), to decrypt ciphertext C and receive plain text T we need to perfrom below operation:

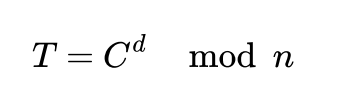
Task overview

We are provided with file values, which contains: ciphertext, big interger n and exponent e. Our task is to decrypt the ciphertext.

Factorisation of n

I used factordb.com to check if n value was already cracked, and lucky for us, it was!

p = 1617549722683965197900599011412144490161 
q = 475693130177488446807040098678772442581573

Our objective for now is to determine value of private component d, however without knowing eulers totient, we can’t do that. So now, using formula mentioned in RSA Overview we can calculate it, and then we can move on to d value.

Exploit

from Crypto.Util.number import inverse

p = 1617549722683965197900599011412144490161 
q = 475693130177488446807040098678772442581573
n = p*q
e = 65537
c = 8533139361076999596208540806559574687666062896040360148742851107661304651861689


def calculate_eulers_totient(p,q):
    return (p-1)*(q-1)

def calculate_d(eulers_totient,e):
    return inverse(e, eulers_totient)

def decrypt(c,d,n):
    return pow(c,d,n)

if __name__ == '__main__':
    eulers_totient = calculate_eulers_totient(p,q)
    d = calculate_d(eulers_totient, e)
    T = decrypt(c,d,n)
    print(bytearray.fromhex(hex(T)[2:]).decode())

Final flag: picoCTF{sma11_N_n0_g0od_45369387}